Co-authored by @164zheng & @keccak255 (Titania Research). Thanks to @barnabe, @Julian, @banr1, and Alphaist for their valuable comments and discussions. This research was supported by an Ethereum Foundation ESP grant (FY24-1744).
TL;DR
If the top builder in a slot auction can credibly commit to skipping any block auction, they can incentivize the proposer to choose the slot auction. This strategy can increase the builder’s profit by reducing competition and lowering required bids. As a result, slot auctions can satisfy the No Trusted Advantage more often than expected. Such commitment reshapes incentives and changes the proposer’s optimal choice.
Introduction
As part of the ePBS discussion, the format of the auction by which block builders obtain the right to construct execution blocks is under debate. There are two canonical in-protocol auctions: block auction and slot auction.
A block auction is an auction where the proposer commits to an execution payload at the end of the auction. For example, MEV-boost is this kind of auction style. In a block auction, the builder must commit the specific block payload when submitting the bid.
In contrast, a slot auction is an auction where the proposer does not commit to a specific payload but instead to a specific builder at the end of the auction. In this case, the builder does not need to submit the execution payload at the time of the bid. The winning builder submits the execution payload afterward. Compared to block auctions, slot auctions have the advantage of revenue smoothing because builders bid on expected value, and extreme MEV spikes are averaged out over time.
On the other hand, slot auctions have been criticized for lacking the No Trusted Advantage property. No Trusted Advantage means that the proposer has no incentive to sell the right to construct the block out of protocol. They point out that block auctions are expected to yield higher returns for proposers than slot auctions. (When To Sell Your Blocks) Thus, even if proposers can commit in-protocol to slots, they may still choose to hold out-of-protocol block auctions to sell the right to construct blocks.
This research post reexamines the conditions under which slot auctions satisfy No Trusted Advantage. In particular, we show that when the builder capable of producing the highest expected-value block in the slot auction can commit to not participating in the block auction, they have an incentive to make such a commitment, leading the proposer to choose the slot auction.
Note that this post stays at the level of abstract mechanism design; we leave client-side engineering details aside. What matters for the model is the information each builder has when bidding. In a block auction, a builder has already simulated a concrete payload and knows the exact value it can realize. In a slot auction, by contrast, the builder sees only a rough statistical expectation. (In practice, slot-auction builders may observe weak signals, but not enough to pin down the value precisely. For clarity we model the slot case as if they know only their prior mean.)
Model
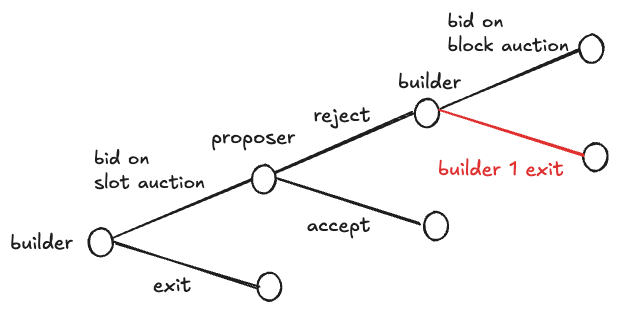
We analyze the proposer’s choice between block and slot auctions using the framework of an extensive-form game in game theory. We first model the behavior and payoffs of the proposer and builders. Then we analyze two cases—without commitment and with commitment—and identify when the builder’s commitment is profitable.
We consider the following extensive-form game:
Players:
One proposer and nn builders i \in \{1, ..., n\} \equiv Ni∈{1,...,n}≡N.
The proposer sells the right to construct a block at slot kk through an auction among nn builders b_ibi.
Preferences and values
All players are risk-neutral with quasi-linear utility. The value of the block that builder ii can build in a block auction is v_i^bvbi, drawn from a distribution function F_i^bFbi. In a slot auction, their block value is v_i^svsi, drawn from a distribution F_i^sFsi. These are mutually independent and independent across builders.
Suppose builder 1 has the highest expected slot value and builder ii has ii -th highest expected slot value, E[v_1^s] \geq ... \geq E[v_n^s]E[vs1]≥...≥E[vsn]. (E[\cdot]E[⋅] denotes the expected value.)
Timeline
The extensive-form game unfolds as follows:
Stage 0: Commitment
Builder 1 may commit not to enter a block auction.
Stage 1 – slot auction
An English (ascending-bid) slot auction is held first. Each builder only knows their expected block value E[v_i^s]E[vsi] at this stage.
Mechanics
- The auction opens at time 0 with a standing price of 0.
- Until the announced deadline T_sTs, any builder may place a new standing bid of any size, provided it strictly exceeds the current standing bid.
- A builder may abstain by never submitting a bid (or by ceasing to bid once the price is too high).
- When the deadline T_sTs arrives, bidding stops immediately.
- The highest standing bid at that instant—denote it $p_s$—wins, and its owner ww becomes the provisional slot winner.
- No payment is collected and no payload is delivered yet.
Each builder can choose to bid x_i^sxsi or exit from the auction.
Stage 2 – proposer’s choice
After observing the final slot price p_sps, the proposer chooses:
Accept Slot Auction: The winner pays p_sps to the proposer and earns the right to build a block of the slot. The builder’s payoff is v_i^s - p_svsi−ps if they win; otherwise 0.
Reject Slot Auction and open a Block auction: The slot result is void and the game moves to a block auction.
Stage 3 – block auction (executed only if the proposer rejected the slot result)
If the proposer opened an English block auction, each builder now learns its exact block value v_i^bvbi, and then they participate in the block auction.
The winner of the block auction pays p_bpb to the proposer and receives the value of the block it submitted. The builder’s payoff is v_i^b - p_bvbi−pb.
Result
We analyze the equilibrium of this game using backward induction.
Stage 3 – block auction
In English auctions, each builder bids up to the point where their payoff becomes zero in the equilibrium. Let the set of entrants in the auction be M_b \subseteq N.Mb⊆N.
In block auctions, each builder knows their actual block value and bids up to it. The winner — builder yy with the highest block value — wins the auction at the second-highest value among participants:
E[p_b] = R_{b}(M_b) = E[\text{second}(v_j^b)_{j\in M_b}]E[pb]=Rb(Mb)=E[second(vbj)j∈Mb].
Builders decide whether to participate in the auction. In block auctions, every eligible builder obtains a positive expected surplus by bidding, so all eligible builders enter.
If builder 1 has committed, she is ineligible. Thus, the payoff for the proposer is
R_{b}(N)Rb(N) without commitment, and R_b(N \setminus \{1\})Rb(N∖{1}) with commitment.
The payoff for an each builder ii is E\!\bigl[\max(v_i^{b}-\text{second}(v_j^b)_{j\in M_b}, 0)\bigr]E[max(vbi−second(vbj)j∈Mb,0)] .
Stage 2 - proposer’s choice
Let p_sps be the winning slot bid recorded in Stage 1. The proposer accepts the slot result if and only if p_s \geq R_bps≥Rb. Otherwise, she rejects and runs the block auction.
Stage 1 – slot auction
Without any commitment
Note that the proposer will reject any slot outcome that yields less revenue than the expected block auction’s value R_b(N)Rb(N) in stage 2; hence R_b(N)Rb(N) acts as an implicit reserve price.
Every builder ii compares the current price with her own expected slot value E[v_i^s]E[vsi]
If the auction price reaches R_b(N)Rb(N), the proposer will accept the slot auction result. Then, each builder has an incentive to raise the price to her own expected slot value E[v_i^s]E[vsi], because otherwise she ends up losing the auction and her payoff becomes zero. As a result, builder 1 wins the auction with the price E[v_2^s]E[vs2]. In this case, builder 1’s payoff is E[v_1^s] - E[v_2^s]E[vs1]−E[vs2].
So, no builders except builder 1 have an incentive to make a bid above R_b(N)Rb(N) when the auction opens because that makes their payoff zero and they can earn a positive profit in the block auction. Only builder 1 has an incentive to bid above R_b(N)Rb(N) if and only if her payoff of the slot auction exceeds that of the block auction:
E[v_1^s] - \max(E[v_2^s], R_b(N)) \geq E\!\bigl[\max(v_1^{b}-\text{second}(v_j^b)_{j\in N}, 0)\bigr]E[vs1]−max(E[vs2],Rb(N))≥E[max(vb1−second(vbj)j∈N,0)]
if it holds, builder 1’s payoff is E[v_1^s] - \max(E[v_2^s], R_b(N))E[vs1]−max(E[vs2],Rb(N)) .
With builder 1’s commitment
In this case, the implicit reserve price becomes R_b(N \setminus \{1\})Rb(N∖{1}) because builder 1 commits not to participate in the block auction. Thus, builder 1’s payoff becomes
E[v_1^s] - \max(E[v_2^s], R_b(N \setminus \{1\}))E[vs1]−max(E[vs2],Rb(N∖{1}))
Stage 0 - builder 1’s commitment
The commitment is rational for builder 1 if and only if her expected payoff in the slot auction with the commitment exceeds their expected payoff in the block auction without the commitment:
E[v_1^s]- \max\bigl\{E[v_2^s],\;R_{\text{b}}(N\setminus\{1\})\bigr\} \geq E\bigl[\max(v_1^{b}-\text{second}\{v_j^{b}\}_{j\in N}, 0)\bigr].E[vs1]−max{E[vs2],Rb(N∖{1})}≥E[max(vb1−second{vbj}j∈N,0)].
Overall, define
If U_{\text{slot without commit}} \;\le\; U_{\text{block}} \;\le\; U_{\text{slot with commit}},Uslot without commit≤Ublock≤Uslot with commit,
builder 1’s pledge flips the proposer’s choice from a block auction (without the commitment) to a slot auction (with the commitment).
if U_{\text{slot without commit}} \;\ge\; U_{\text{block}}Uslot without commit≥Ublock,
the proposer would have chosen the slot auction anyway; nevertheless, Builder 1 still benefits from the commitment because it lowers the reserve from R_b(N)Rb(N) to R_b(N \setminus \{1\})Rb(N∖{1}) and increases her surplus by the difference R_b(N) - R_b(N \setminus \{1\})Rb(N)−Rb(N∖{1}) whenever R_b(N \setminus \{1\} ) \geq E[v_2^s]Rb(N∖{1})≥E[vs2].
Discussion
Our results show that a credible builder commitment can flip the proposer from a block auction to a slot auction. If the builder with the highest expected slot value promises to skip the block auction and posts a big enough slot bid, the proposer earns more from the slot auction, while the builder faces less competition and keeps a larger profit.
Note that if no commitment is made and E[v_i^b] = E[v_i^s]E[vbi]=E[vsi], the builder’s expected revenue in a block auction is higher than in a slot auction.
Proof
When builder 1 commits, the slot auction can—though only in a narrow set of circumstances—deliver higher total revenue. Moreover, if builder 1’s expected payoff in the slot auction exceeds her expected payoff in the block auction, the chance that the proposer will opt for the slot auction rises even further. In addition, the slot format becomes even more attractive—and therefore more likely to be selected—when the builder with the highest slot revenue experiences a larger uplift over her block-auction earnings than any of the other builders.
Furthermore, as builders merge and the field becomes more concentrated, the expected second-highest block value—the proposer’s fallback or “reserve” price—falls. A lower reserve makes builder 1’s commitment easier to clear, so the commitment becomes more powerful and the slot auction is correspondingly more likely to be chosen.
The hard part is making the builder’s commitment credible. In practice, this may need a large on-chain bond (for example, through an EigenLayer AVS) or a hardware attestation that is costly to break. Who commits first also matters: if the proposer first commits to block auctions, the builder’s promise loses power; if the builder commits first, the proposer is pushed toward the slot auction.
It would also be interesting to investigate what conclusions would arise if we assumed interdependent values and modeled the competition as an ascending auction. Under inter-dependent values, an ascending-price auction reveals signals as the clock ticks, raising the proposer’s fallback price while deeper winner’s-curse shading cuts each builder’s surplus. A “slot-only” commitment could still tip the proposer toward the slot auction, but only if the top builder’s private edge clears this higher bar—the feasible window narrows, yet need not vanish. This remains a conjecture; a formal model is deferred to future work.
Finally, because auctions repeat every 12 seconds with mostly the same builders, the real setting is a repeated game. Studying those long-run dynamics—and testing them with past bid data—is an important task for future research.